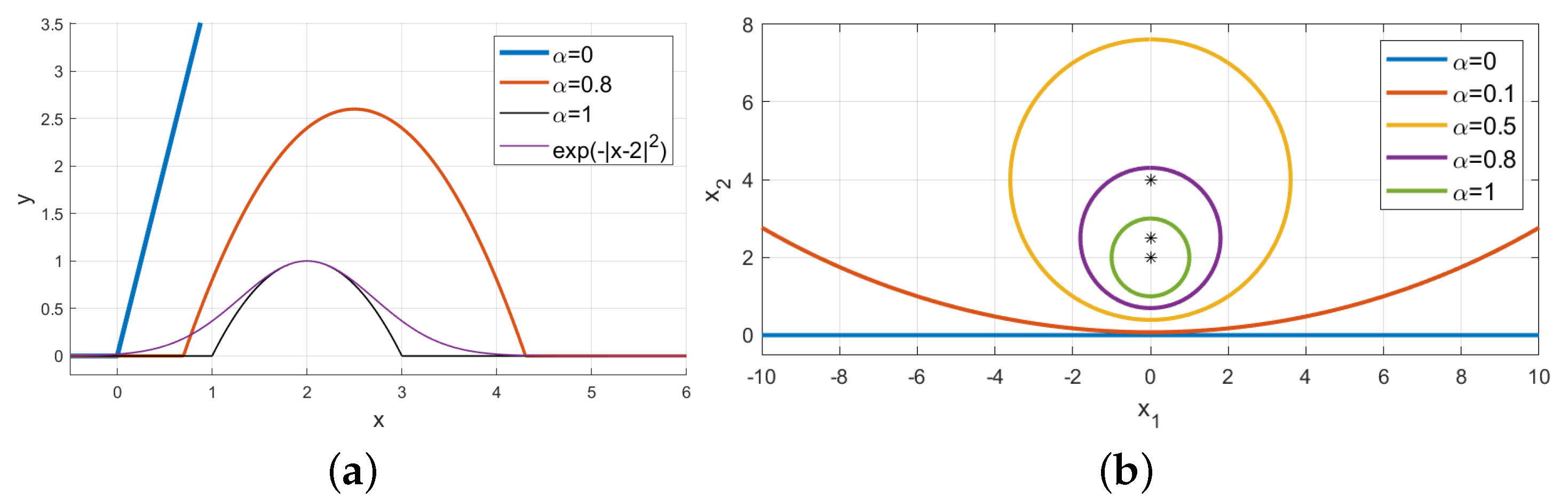
Radial basis functions with compact support for elastic registration of medical images | Semantic Scholar
LECTURE 3: SMOOTH FUNCTIONS 1. Smooth Functions Definition 1.1. Let (M,A) be a smooth manifold, and f : M → R a function. (1)

True/false : The Space of all continiuos real valued functions with compact support with supnorm metric is complete . - Mathematics Stack Exchange

Color online) Functions φǫ with compact support defined in Eq.(28) for... | Download Scientific Diagram

Evolution of a compact support function as initial condition under the... | Download Scientific Diagram

calculus - An example of an infinitely differentiable function with compact support - Mathematics Stack Exchange

SOLVED: Problem 11: Prove that the space C (smooth functions of compact support) is dense in L (with respect to the L topology) by following the steps below. 1. Given f ∈

Advances in LAM 3D-VAR formulation Vincent GUIDARD Claude FISCHER Météo-France, CNRM/GMAP. - ppt download

Convert implicit surface defined with global support to compact support - Rodolphe Vaillant's homepage

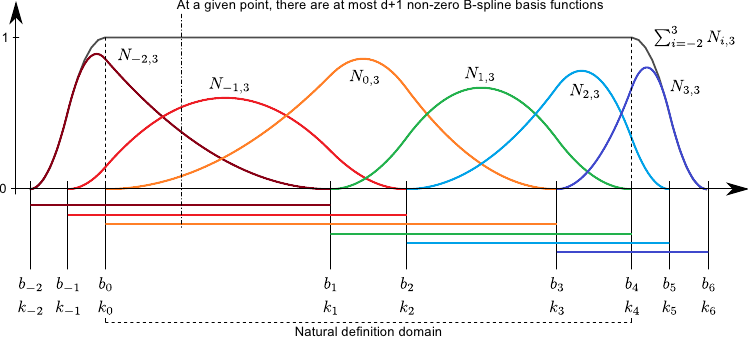


![PDF] Building new kernel family with compact support, in scale-space | Semantic Scholar PDF] Building new kernel family with compact support, in scale-space | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/30d67331ea773eff77c8ce706003495281a54d38/6-Figure1-1.png)